Forums
|
Forums >> Revit Building >> Technical Support >> How to make the top of the wall not horizontal?
|
|
|
active
Joined: Wed, Mar 24, 2010
11 Posts
 |
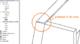
Hi everyone.There's my first question that I couldn't find answer for. I'm making a slope wall, so how to make top and bottom of the wall not horizontal?Firstly, I tried to make sloped mass, with sloped top and bottom. I put a wall by picking the face of the mass. I got the slope wall, but bottom and top of the wall were horizontal.Then I thought that if I void something in mass, it became voided also in the wall. So I made a mass with horizontal top, then I voided the top of this mass so it became sloped. Then I put the wall by using "pick face" tool but the wall ignored this void (only this void, another voids worked well) and still the top of the wall became horizontal. Is there anyone who knows how solve this problem?P.S. I thought maybe I can add thin line of the roof at the toop of the wall, so it can be sloped, and then somehow to try to join them, but I hope there is way how to make the wall with sloped top and bottom.P.S.S. I'm attaching few pictures to be more clear.
|
This user is offline |
|
 | |
|
|
site moderator|||
Joined: Tue, May 16, 2006
13079 Posts
 |
Don't use a mass. Just place a regular wall then edit the wall profile from an elevation view.
|
This user is offline |
|
 |
|
active
Joined: Wed, Mar 24, 2010
11 Posts
 |
Thanks to you answer.But I can edit profile only in front and back view of the wall. I can't do the same in the sides
|
This user is offline |
|
 |
|
site moderator|||
Joined: Tue, May 16, 2006
13079 Posts
 |
Sorry - I responded to your question without looking at your images. You do need the mass to make a sloping wall. You can make yor wall taller than it needs to be then use an in-place void to cut off the excess wedge. That void might cut all your walls at the same time... just a big plane (with thickness). The roof might work but not sure with walls by face.
|
This user is offline |
|
 |
|
active
Joined: Wed, Mar 24, 2010
11 Posts
 |
I've wrote that I tried this way, and I't didn't work. Now I tried it one more time, making more taller mass, then voiding the top as I need but wall ignored this void and it still with horizont top...
|
This user is offline |
|
 |
|
site moderator|||
Joined: Tue, May 16, 2006
13079 Posts
 |
You are having a process issue. Before finishing the void, you have to select the objects it cuts. I would also make the void a wall category.
|
This user is offline |
|
 |
|
active
Joined: Wed, Mar 24, 2010
11 Posts
 |
Do you tried it? I don't know what to do...As I understood, I should to do this that way:1. make mass in place2. make it with a slope I need, but taller ( for example I need 5 meters tall wall and I make slope mass 7 meters)3. then I make few voids (like niches (for example for balconies)), and make one void at the top of the mass, so it has sloped top. I have mass exactly as I want to have the wall4. now I click finish mass5. then I add the wall using pick a face tool6. And I got the wall as I need (with all voids for niches), but the top still horizontal.at which point I miss something?
|
This user is offline |
|
 |
|
site moderator|||

Joined: Tue, May 22, 2007
5921 Posts
 |
Watch the video: http://screencast.com/t/hkQCScCxpf
-----------------------------------
I Hope and I Wish to LEARN more, and more, and more.... REVIT |
This user is offline |
|
 |
|
active
Joined: Wed, Mar 24, 2010
11 Posts
 |
Thanks, you solved my problem ;] I just didn't use the "cut" function
|
This user is offline |
|
 |
|
site moderator|||

Joined: Tue, May 22, 2007
5921 Posts
 |
WWhub told you that in his last post: " Before finishing the void, you have to select the objects it cuts"
-----------------------------------
I Hope and I Wish to LEARN more, and more, and more.... REVIT |
This user is offline |
|
 |
 |
Similar Threads |
|
Top Finish on Walls |
Revit Building >> Technical Support
|
Wed, Nov 29, 2017 at 1:55:05 PM
|
7
|
|
[Help] Make a wall connect close to the top of the roof |
Revit Building >> Technical Support
|
Fri, Apr 24, 2015 at 12:45:03 AM
|
5
|
|
problem with horizontal mullion |
Revit Building >> Technical Support
|
Mon, Oct 31, 2011 at 2:44:39 PM
|
2
|
|
Horizontal Wall or Wrapping Floor |
Revit Building >> Technical Support
|
Mon, Jan 21, 2008 at 3:40:31 PM
|
2
|
|
How do i make an allternating horizontal 4" and 8" .pat file in notepad??? |
Revit Building >> Technical Support
|
Tue, Sep 6, 2011 at 6:32:54 PM
|
1
|
 |
|
Site Stats
Members: | 2019228 | Objects: | 22958 | Forum Posts: | 152184 | Job Listings: | 3 |
|